Python Numbers Explained

Let’s be honest—most of us still have trust issues from high school math. Remember that one teacher who said, “This will be useful in real life” while you were solving for x? Yeah… fast-forward 10 years and the only “x” you’re solving for is why your code keeps throwing TypeError.

But here’s the thing: Python numbers are not scary monsters. They’re more like roommates—sometimes chill, sometimes weird, sometimes “why are you taking all the memory, bro?” But once you understand them, they’ll help you do everything from calculating your pizza bill 🍕 to running machine learning models.

So grab your favorite drink ☕, because today we’re deep-diving into Python numeric types: int, float, and complex, with jokes, examples, and zero math trauma.

Python Number Data Types Overview

Python has three built-in numeric types:

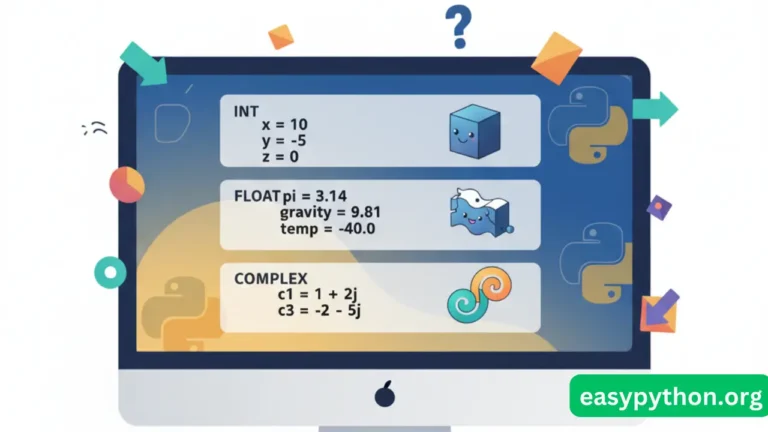
• int → Whole numbers (positive, negative, or zero).
• float → Decimal numbers with floating precision.
• complex → Numbers with a real part and an imaginary part. (Yes, imaginary—don’t worry, they won’t ghost you).

👉 If you’re new to Python, check out this Python data types overview first—it’s like a warm-up stretch before lifting heavy coding weights.

Integers in Python (int)

Integers are like that reliable old friend—solid, predictable, and always there.

x = 42
y = -99
z = 0

print(type(x))   # <class 'int'>

x = 42
y = -99
z = 0

print(type(x))   # <class 'int'>

Key Facts about Integers

• No size limit (Python integers are like a buffet—eat as much as you want).
• Used for counters, loops, indexing, or anytime decimals are unnecessary.
• They’re immutable (change value, new int object is created).

💡 Pro Tip: Unlike C or Java, Python integers don’t overflow—you can go from 42 to 4200000000000000000 without Python fainting.

Floating-Point Numbers (float)

Now here’s where Python starts acting like that one flaky friend. Floats deal with decimals, but because computers use binary, they can’t always store decimals precisely.

a = 3.14
b = 2.0
c = -0.0001

print(type(a))   # <class 'float'>

a = 3.14
b = 2.0
c = -0.0001

print(type(a))   # <class 'float'>

⚠️ The Float Problem

print(0.1 + 0.2)  # 0.30000000000000004 

print(0.1 + 0.2)  # 0.30000000000000004 

Yep, that’s not a bug. It’s just how binary floating-point works. Even Python has to live with math’s quirks. If you’re working with money 💵, you should use decimal.Decimal.

👉 Want a deeper look at strings and number conversions? Here’s a fun Python string tutorial to help you out.

Complex Numbers (complex)

Complex numbers sound like an unnecessary extra feature… until you realize scientists and engineers actually love them.

z = 2 + 3j
print(z.real)   # 2.0
print(z.imag)   # 3.0

z = 2 + 3j
print(z.real)   # 2.0
print(z.imag)   # 3.0

• real → gives the real part.
• imag → gives the imaginary part.
• Operations like addition, multiplication, and exponentiation are supported.

If you’re working on AI, simulations, or solving equations with imaginary parts, complex numbers are your secret weapon.

Type Conversion Between Numbers

Python makes converting between numeric types super easy:

x = int(3.9)     # 3
y = float(42)    # 42.0
z = complex(5)   # (5+0j)

x = int(3.9)     # 3
y = float(42)    # 42.0
z = complex(5)   # (5+0j)

• int() → Truncates decimals.
• float() → Converts integers to decimals.
• complex() → Converts int or float into complex.

👉 This comes in handy when taking user input since all input is str by default.

Built-in Functions for Numbers

Python comes with a buffet of built-in functions to make life easier:

• abs(-7) → 7
• round(3.14159, 2) → 3.14
• pow(2, 3) → 8
• divmod(9, 4) → (2, 1)

👉 Full list? Check out the Python built-in functions guide.

Python Numbers Methods & Functions Cheatsheet

Decimal and Fraction Types

Floats are fine until you’re calculating salaries or taxes. Then precision matters.

• decimal.Decimal → Exact decimal representation (great for financial apps).
• fractions.Fraction → For exact rational arithmetic.

from decimal import Decimal
from fractions import Fraction

print(Decimal('0.1') + Decimal('0.2'))  # 0.3
print(Fraction(1, 3) + Fraction(1, 3))  # 2/3

from decimal import Decimal
from fractions import Fraction

print(Decimal('0.1') + Decimal('0.2'))  # 0.3
print(Fraction(1, 3) + Fraction(1, 3))  # 2/3

Common Gotchas with Python Numbers

1. Float precision issues (0.1 + 0.2 ≠ 0.3).
2. Division in Python 3 → / always returns float. Use // for integer division.
3. Complex numbers can’t be ordered → 2+3j < 3+2j will throw an error.

Where to Go Next

Numbers are just one piece of the Python puzzle. Once you’ve conquered them, check out:

• Python sets explained
• Python collection types
• Learn Python for beginners
• Or even a list of the best Python books if you’re the “coffee + paperback” type.

Final Thoughts

Python numbers aren’t scary—ints are reliable, floats are moody, and complex numbers are nerdy but cool. Mastering them makes your code stronger, your math teacher prouder, and your debugging sessions shorter.

So go ahead, play with Python numbers. Just remember: if 0.1 + 0.2 != 0.3 keeps you up at night… it’s not you, it’s binary.